Bloom filters are one of my favorite data structures! They are faster than a HashMap, memory-wise more efficient than a HashMap, and still provide exciting value.
Bloom filters are probabilistic data structures that track if a given KEY has been seen before! What in the world does that mean? It means that Bloom filters can only answer in two ways:
- The given KEY has NEVER been seen before!
- The given KEY has PROBABLY been seen before!
The second one is strange. In computer science we expect to get straight answers of yes or no, so to have PROBABLY feels surprising. So let’s dive into when Bloom filters are useful, how they work, and some of the trade-offs associated with them.
When are they useful?
How can a probabilistic answer be useful? Imagine you have an expensive operation, such as searching for some data. Also, assume that most of the time, the search will come up with nothing.
That means that most of the time, we are wasting time searching for something that does not exist. But we must search just on the off-chance that it could exist.

If we could only get a hint that something for sure is not in a set, we could save ourselves a whole bunch of time. This is exactly what Bloom filters are good at. They can short circuit doing a lot of work which will come up with nothing.
When a Bloom filter says we may have an item, we still need to do a search on the off chance that the bloom filter is wrong, but this is a rare case.
How Bloom filters work
Bloom filters work similarly to HashMaps. But instead of storing the KEY and VALUE, they only store whether a given KEY has been seen.
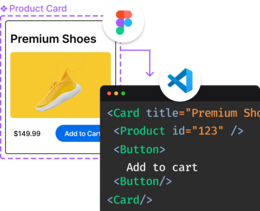
The first step is to convert the KEY into a hashCode. This is done with a hashing function, which is beyond the scope of this article. A hashing function is a pseudo-random number generator where the KEY is the seed. A hashCode is just a number that has random distribution.
We generate the hashCode as an index into a bit array. A hashCode number is too large to be used as an index, so we module the hashCode with bit array length to get an index.
We then use the index in the bit array to store 1. That is it.
Notice we said it is a bit array not an array of bits. 8 bits make a byte. So a single byte can store 8 separate bits 1 and 0s. This is what makes Bloom filters so efficient.
Collisions
There are two sources of collisions:
- The hashing function is not perfect and so two different KEYs can have the same
hashCode. Actually, the number of possible KEYs is essentially infinite, whereas thehashCodeis a 64-bit integer, so you are guaranteed collisions. - The
hashCodeis way too big, so we fold it onto a smaller bit array. The folding operation (module) further increases the possibility of collision.
So what do we do about collisions? Nothing! That is what makes the Bloom filter probabilistic. Seeing that a particular KEY has a 1 in the bit array, it is unclear if that 1 came from our KEY or some other KEY that either had the same hashCode or folder to the same bit array index.
Reading values
Reading from the Bloom filter is the same as writing except instead of setting a bit in the bit array we read that bit:
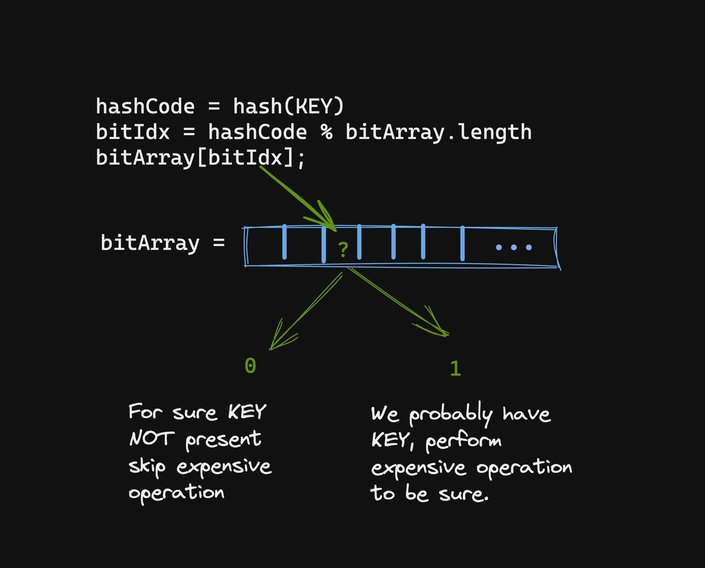
A lack of 1 at that location implies that we could not have possibly seen that KEY before, whereas the presence of 1 implies that we may have seen it before.
Here the “may” comes from the fact that we can’t distinguish if we have seen that specific KEY or the same other KEY with the same hashCode or the same fold to the index.
Fine-tuning performance
There are a few knobs that a Bloom hash can do to make it perform better (fewer false positives.)
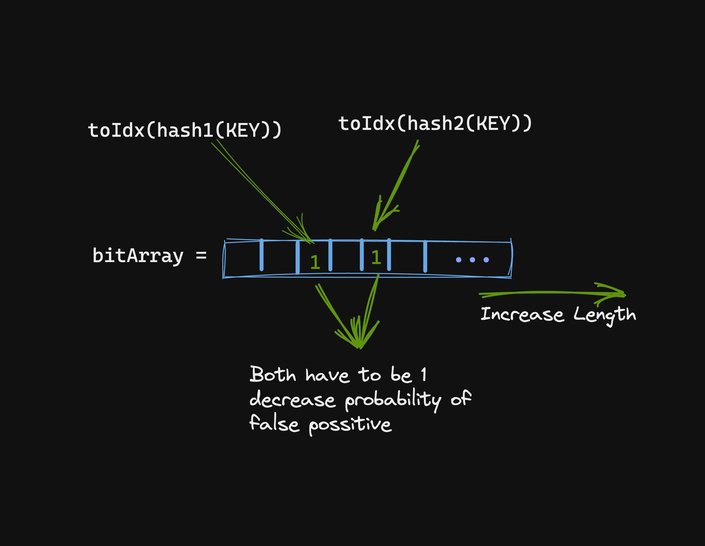
The most obvious one is to increase the bit array length. As the bit array gets longer, the hashing spaces increase and it is less likely that a hashCode will fold to the same index.
Another trick is to add multiple hash functions. Each hashing function would produce a different hashCode which would then fold onto a different location. We can then ensure that all bits have been present to decrease the probability of collision.
Removal
Removing KEYs from a Bloom filter is impossible because we don’t know how many KEYs have mapped to a particular bit array index.
However, a counting Bloom filter data structure can support removals. At the expense of trading bit-array for an array of numbers, instead of storing a bit, we can now store a count. The addition of a KEY increments a count and removal decrements it.
Bloom Filters in Real Life
My favorite use of Bloom filter in real life was in Angular’s Ivy runtime.
Angular needs to resolve injector keys. The injector providers are first resolved by the component hierarchy and then by the module injector. The vast majority of injectables will be found in the module injector. But we can’t skip the component hierarchy, just in case.
Doing a full search of the component hierarchy would have been time-consuming, so Bloom filters to the rescue! Each component had two bloom filters of 8 numbers each. Yes, eight numbers. That is small.
One Bloom filter would answer if the injection KEY could be found in the current component. And second Bloom filter would answer if the parent component could have the KEY. This way, the injector could quickly bail out from searching the component hierarchy and jump to the module injector.
On the off-chance that the component hierarchy had the Injector KEY, it was a quick search because the Component Bloom filter would tell us if we should look at the component or go to the parent.
Conclusion
Bloom filters are a type of probabilistic data structure that determines whether a given key has been seen before.
They are faster and memory-wise more efficient than hash maps and are useful when searching for data that might not exist in a large set.
A Bloom filter can answer with certainty if it did not see a KEY, but can only say that it is likely that it has seen it.
This information can be used to short-circuit expensive operations to gain performance.
Introducing Visual Copilot: convert Figma designs to high quality code in a single click.